Спектральный анализ сигналов Хабрахабр. Не так давно товарищ Makemanописывал, как с помощью спектрального анализа можно разложить некоторый звуковой сигнал на слагающие его ноты. Давайте немного абстрагируемся от звука и положим, что у нас есть некоторый оцифрованный сигнал, спектральный состав которого мы хотим определить, и достаточно точно. Под катом краткий обзор метода выделения гармоник из произвольного сигнала с помощью цифрового гетеродинирования, и немного особой, Фурье магии. Итак, что имеем. Файл с отсчетами оцифрованного сигнала. Известно, что сигнал представляет собой сумму синусоид со своими частотами, амплитудами и начальными фазами, и, возможно, белый шум. Что будем делать. JPG' alt='Программа Спектральный Анализатор' title='Программа Спектральный Анализатор' />Описание Бесплатный анализатор звука с шагом 8 kHz. Обзор программы SpectralView Analyzer Анализатор звука. Обзор спектрального анализатора Voxengo Span Plus 8 Mb, SpectraPLUS v. Обладающая сверх высокой резолюцией анализа, эта. Мощная программа для анализа звука и шума в реальном времени. Идеальна для работы с аудиосигналами любого уровня сложности. SpectraLab v. 4. 32. Наверное лучшая программа звукового анализа спектральный анализатор, осциллограф, фазометр. Все необходимые. Использовать спектральный анализ для того, чтобы определить количество гармоник в составе сигнала, а для каждой амплитуду, частоту далее в контексте числа длин волн на длину сигнала, начальную фазу наличиеотсутствие белого шума, а при наличии, его СКО среднеквадратическое отклонение наличиеотсутствие постоянной составляющей сигнала вс это оформить в красивенький PDF отчт с блэкджеком и иллюстрациями. Будем решать данную задачу на Java. Матчасть. Как я уже говорил, структура сигнала заведомо известна это сумма синусоид и какая то шумовая составляющая. Так сложилось, что для анализа периодических сигналов в инженерной практике широко используют мощный математический аппарат, именуемый в общем Фурье анализ. Давайте кратенько разберм, что же это за зверь такой. Немного особой, Фурье магии. Не так давно, в 1. Жан Батист Жозеф Фурье показал, что любую функцию, удовлетворяющую некоторым условиям непрерывность во времени, периодичность, удовлетворение условиям Дирихле можно разложить в ряд, который в дальнейшем получил его имя ряд Фурье. В инженерной практике разложение периодических функций в ряд Фурье широко используется, например, в задачах теории цепей несинусоидальное входное воздействие раскладывают на сумму синусоидальных и рассчитывают необходимые параметры цепей, например, по методу наложения. Существует несколько возможных вариантов записи коэффициентов ряда Фурье, нам же лишь необходимо знать суть. Разложение в ряд Фурье позволяет разложить непрерывную функцию в сумму других непрерывных функций. Инструкция Старлайн А92. И в общем случае, ряд будет иметь бесконечное количество членов. Дальнейшим усовершенствованием подхода Фурье является интегральное преобразование его же имени. Преобразование Фурье. В отличие от ряда Фурье, преобразование Фурье раскладывает функцию не по дискретным частотам набор частот ряда Фурье, по которым происходит разложение, вообще говоря, дискретный, а по непрерывным. Давайте взглянем на то, как соотносятся коэффициенты ряда Фурье и результат преобразования Фурье, именуемый, собственно, спектром. Небольшое отступление спектр преобразования Фурье в общем случае, функция комплексная, описывающая комплексные амплитуды соответствующих гармоник. Т. е., значения спектра это комплексные числа, чьи модули являются амплитудами соответствующих частот, а аргументы соответствующими начальными фазами. Программа Спектральный Анализатор' title='Программа Спектральный Анализатор' />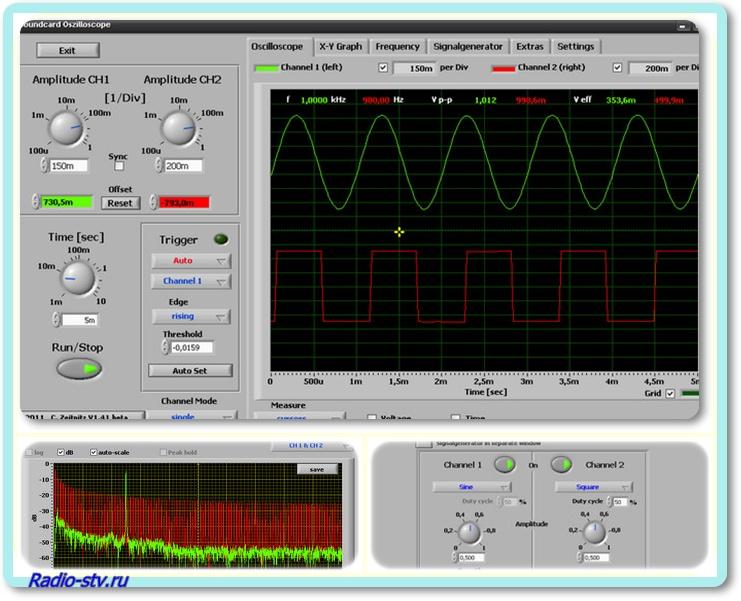На практике, рассматривают отдельно амплитудный спектр и фазовый спектр. Рис. Соответствие ряда Фурье и преобразования Фурье на примере амплитудного спектра. Легко видно, что коэффициенты ряда Фурье являются ни чем иным, как значениями преобразования Фурье в дискретные моменты времени. Однако, преобразование Фурье сопоставляет непрерывной во времени, бесконечной функции другую, непрерывную по частоте, бесконечную функцию спектр. Как быть, если у нас нет бесконечной во времени функции, а есть лишь какая то записанная е дискретная во времени часть Ответ на этот вопрос дат дальнейшей развитие преобразования Фурье дискретное преобразование Фурье ДПФ. Дискретное преобразование Фурье призвано решить проблему необходимости непрерывности и бесконечности во времени сигнала. По сути, мы полагаем, что вырезали какую то часть бесконечного сигнала, а всю остальную временную область считаем этот сигнал нулевым. Математически это означает, что, имея исследуемую бесконечную во времени функцию ft, мы умножаем ее на некоторую оконную функцию wt, которая обращается в ноль везде, кроме интересующего нас интервала времени. Если выходом классического преобразования Фурье является спектр функция, то выходом дискретного преобразования Фурье является дискретный спектр. И на вход тоже подаются отсчты дискретного сигнала. Остальные свойства преобразования Фурье не изменяются о них можно прочитать в соответствующей литературе. Нам же нужно лишь знать о Фурье образе синусоидального сигнала, который мы и будем стараться отыскать в нашем спектре. В общем случае, это пара дельта функций, симметричная относительно нулевой частоты в частотной области. Рис. Амплитудный спектр синусоидального сигнала. Я уже упомянул, что, вообще говоря, мы рассматриваем не исходную функцию, а некоторое е произведение с оконной функцией. Тогда, если спектр исходной функции Fw, а оконной Ww, то спектром произведения будет такая неприятная операция, как свртка этих двух спектров FWw Теорема о свртке. На практике это означает, что вместо дельта функции, в спектре мы увидим что то вроде этого Рис. Эффект растекания спектра. Этот эффект именуют также растеканием спектра англ. А шумы, появляющиеся вследствие растекания спектра, соответственно, боковыми лепестками англ. Для борьбы с боковыми лепестками применяют другие, непрямоугольные оконные функции. Основной характеристикой эффективности оконной функции является уровень боковых лепестков д. Б. Сводная таблица уровней боковых лепестков для некоторых часто используемых оконных функций приведена ниже. Оконная функция. Уровень боковых лепестков д. БОкно Дирихле прямоугольное окно 1. БОкно Ханна 3. 1. БОкно Хэмминга 4. БОсновной проблемой в нашей задаче является то, что боковые лепестки могут маскировать другие гармоники, лежащие рядом. Отдельные спектры гармоник. Видно, что при сложении приведнных спектров, более слабые гармоники как бы растворятся в более сильной. Рис. Чтко видна лишь одна гармоника. Нехорошо. Другой подход к борьбе с растеканием спектра состоит в вычитании из сигнала гармоник, создающих это самое растекание. То есть, установив амплитуду, частоту и начальную фазу гармоники, можно вычесть е из сигнала, при этом мы уберм и дельта функцию, соответствующую ей, а вместе с ней и боковые лепестки, порождаемые ей. Другой вопрос состоит в том, как же точно узнать параметры нужной гармоники. Недостаточно просто взять нужные данные из комплексной амплитуды. Комплексные амплитуды спектра сформированы по целым частотам, однако, ничто не мешает гармонике иметь и дробную частоту. В этом случае, комплексная амплитуда как бы расплывается между двумя соседними частотами, и точную е частоту, как и другие параметры, установить нельзя. Для установления точной частоты и комплексной амплитуды нужной гармоники, мы воспользуемся примом, широко применяемым во многих отраслях инженерной практики гетеродинирование. Посмотрим, что получится, если умножить входной сигнал на комплексную гармонику ExpIt. Спектр сигнала сдвинется на величину w вправо. Этим свойством мы и воспользуемся, сдвигая спектр нашего сигнала вправо, до тех пор, пока гармоника не станет ещ больше напоминать дельта функцию то есть, пока некоторое локальное отношение сигналшум не достигнет максимума. Тогда мы и сможем вычислить точную частоту нужной гармоники, как w. Иллюстрация изменения спектра в зависимости от частоты гетеродина показана ниже. Программы для проведения измерений на базе ПК. Обнаружен блокировщик рекламы. Сайт Паяльник существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Как это сделать Призовой фондна ноябрь 2. Тестер компонентов LCR T4.